When Fourier fails: Finite difference stencils
In today's post, we show that high-order finite-difference stencils become inaccurate. You may find the accompanying Python code on GitHub.
Intro
This series of posts looks into different strategies for interpolating non-periodic, smooth data on a uniform grid with high accuracy. For an introduction, see the first post of this series. In the following, we will show that high-order finite differences and accordingly Taylor expansions are not a viable solution. We will create the following plot:
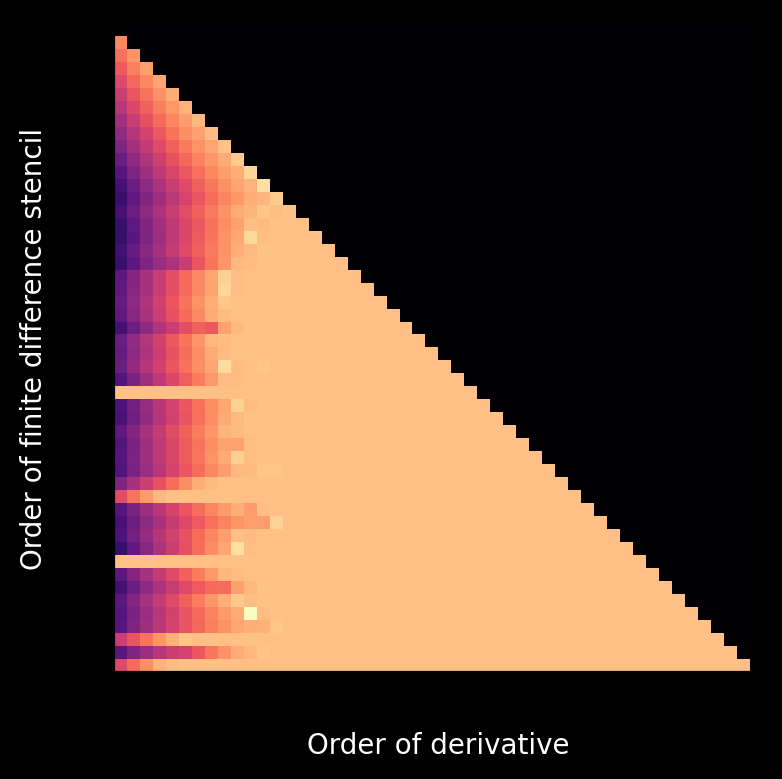
Arbitrary-order finite difference stencils
Finite difference stencils work by discretising differential operators on a discrete grid. They are usually derived by suitable manipulation of the Taylor expansion of given function. On a uniform grid, we can easily derive arbitrarily high-order finite differences. For \(N = 3\), we need to solve the following linear system:
\[\begin{bmatrix} \Delta x & \frac{\Delta x^2}{2!} & \frac{\Delta x^3}{3!} \\ 2\cdot \Delta x & \frac{(2\cdot \Delta x)^2}{2!} & \frac{(2\cdot \Delta x)^3}{3!} \\ 3\cdot \Delta x & \frac{(3\cdot \Delta x)^2}{2!} & \frac{(3\cdot \Delta x)^3}{3!} \end{bmatrix} \cdot \begin{bmatrix} f'(x_0) \\ f''(x_0) \\ f'''(x_0) \end{bmatrix} = \begin{bmatrix} f(x_0 + \Delta x) - f(x_0) \\ f(x_0 + 2\cdot \Delta x) - f(x_0) \\ f(x_0 + 3\cdot \Delta x) - f(x_0) \end{bmatrix}\]The solution vector contains the first, second and third derivative of \(f\) at \(x_0\) with third-order accuracy. This linear system is derived by writing down suitable Taylor expansions of \(f\) with respect to \(x_0\), \(x_0 + \Delta x\), \(x_0 + 2\cdot \Delta x\) etc., solving for the desired derivatives and neglecting higher-order terms. Using this method, forward, backward, centered and irregular finite-difference stencils can be derived.
Instability
However, in practice computing high-order derivatives using this method becomes increasingly inaccurate for higher orders as the introductory figure demonstrates. It shows the error of the derivative of \(f(x) = \exp(x)\) at \(x_0 = 0\) with the derivative approximated using a forward finite difference stencil. Darker shades of purple represent lower errors. For finite difference stencils up to roughly \(12^{th}\) order, the errors for lower-order derivatives decrease. For finite difference stencils with order \(> 12\), even the the estimation of low-order derivatives fails and it is impossible to accurately estimate derivatives with order \(> 12\). Note that the upper right triangle is black since we can only estimate a derivative of order \(N\) with a finite difference stencil of at least order \(N\). The failure of higher-order finite difference stencils is linked to the Runge phenomenon. We cannot approximate \(f\) using high-order polynomials on a uniform discrete grid which is exactly what the Taylor expansion attempts to do. This shows that periodic extensions of non-periodic functions relying on finite differences also suffer from the Runge phenomenon.
Code
The following code computes arbitrary-order forward, backward and centered finite differences and produces the above figure.
import numpy as np
import scipy
import matplotlib.pyplot as plt
def forward_difference_matrix(order, dx):
"""
Create a forward difference matrix of a given order and spacing.
Args:
order (int): The order of the matrix.
dx (float): The spacing between points.
Returns:
numpy.ndarray: The forward difference matrix.
"""
size = order
mat = np.zeros((size, size))
for k in range(1, size + 1):
for j in range(1, size + 1):
mat[j - 1, k - 1] = (j * dx) ** k / np.math.factorial(k)
return mat
def backward_difference_matrix(order, dx):
"""
Create a backward difference matrix of a given order and spacing.
Args:
order (int): The order of the matrix.
dx (float): The spacing between points.
Returns:
numpy.ndarray: The backward difference matrix.
"""
size = order
mat = np.zeros((size, size))
for k in range(1, size + 1):
for j in range(1, size + 1):
mat[j - 1, k - 1] = (-j * dx) ** k / np.math.factorial(k)
return mat
def forward_difference_vector(order, f):
"""
Create a forward difference vector for a given function and order.
Args:
order (int): The order of the difference.
f (numpy.ndarray): The function values.
Returns:
numpy.ndarray: The forward difference vector.
"""
diff = np.zeros(order)
for j in range(1, order + 1):
diff[j - 1] = f[j] - f[0]
return diff
def backward_difference_vector(order, f):
"""
Create a backward difference vector for a given function and order.
Args:
order (int): The order of the difference.
f (numpy.ndarray): The function values.
Returns:
numpy.ndarray: The backward difference vector.
"""
diff = np.zeros(order)
for j in range(1, order + 1):
diff[j - 1] = f[-1 - j] - f[-1]
return diff
def iterative_refinement(A, b, tolerance=1e-12):
"""
Solve a system of linear equations Ax = b using iterative refinement.
Args:
A (numpy.ndarray): The matrix A.
b (numpy.ndarray): The vector b.
tolerance (float): The tolerance for the residual error.
Returns:
numpy.ndarray: The solution vector x.
"""
x = np.linalg.solve(A, b)
residual = b - A @ x
residual_error = np.sum(np.abs(residual))
iteration = 0
while residual_error > tolerance:
correction = np.linalg.solve(A, residual)
x += correction
residual = b - A @ x
residual_error = np.sum(np.abs(residual))
iteration += 1
if iteration > 10:
break
return x
x = np.linspace(0, 10, 64)
def func(x, derivative_order=0):
return np.exp(x)
f = func(x)
N = 50
errors = np.zeros((N, N))
for fd_order in np.arange(N) :
dx = x[1] - x[0]
A = forward_difference_matrix (fd_order + 1, dx)
b = forward_difference_vector (fd_order + 1, f)
Dl = iterative_refinement(A, b)
A = backward_difference_matrix (fd_order + 1, dx)
b = backward_difference_vector (fd_order + 1, f)
Dr = iterative_refinement(A, b)
for derivative_order in range(fd_order):
error = np.abs(func(x[0], derivative_order + 1) - Dl[derivative_order])/(np.abs(Dl[derivative_order])+1e-8)
errors[fd_order, derivative_order] = error
fig, ax = plt.subplots(figsize=(6, 4), dpi=200)
plt.imshow(np.log10(errors + 1e-15), cmap="magma")
plt.ylabel("Order of finite difference stencil")
plt.xlabel("Order of derivative")
plt.gcf().set_facecolor("k")
ax.xaxis.label.set_color('white')
ax.yaxis.label.set_color('white')
fig.tight_layout()
fig.savefig("figures/fd_instability.png", bbox_inches='tight')
fig.show()